2.2.3 直線を任意の比に分割する

（1）直線ABを例えばx：y：zの比で3分割するものとする。Aより任意の直線ACを引き、AC上にAD：DE：EF＝x：y：zとなるような点D,E,Fを求める。

(2）FとBを結び、FBに平行にEE'，DD'を引けば、ABはD'，E'によりx：y：zの比に分割される。

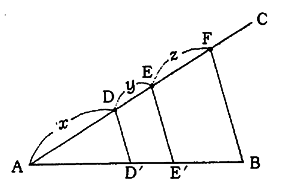
図1.9

3 角度

3.1 角度の等分方法

3.1.1 任意の角度を2等分する

（1）任意の角∠ABCのBを中心として任意半径の弧を描き、BA,BCとの交点D,Eを求める。

（2）各点D,Eを中心として任意の同一半径の弧を描き、両弧の交点Fを求める。BとFを結ぶ直線BFは∠ABCを2等分する。

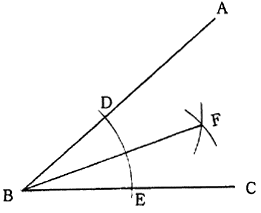
図1.10

3.1.2 直角を3等分する

（1）直角ABCのBを中心として任意半径の弧DEを描き、BA,BCとの交点D,Eを求める。

（2）D,Eを中心としてDEと同一半径の弧を描き、DEとの交点をそれぞれG,Fとする。BG,BFは直角ABCを3等分する。

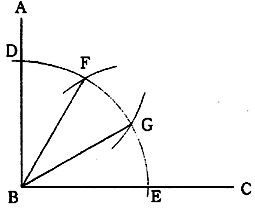
図1.11

3.2 定角に等しい角度を描く方法

（1）定角∠ABCが与えられ、これを他の直線B'C'上に描くものとする。先ず、Bを中心として任意半径の弧を描き、BA,BCとの交点D,Eを求める。

（2）Bを中心としてBEに等しい半径の弧を描き、B'C'との交点をE'とするEを中心としてDEを半径とする弧を描き、前記弧との交点をD'とする。D'、B'を結んで構成される∠D'B'E'は∠ABCに等しい。

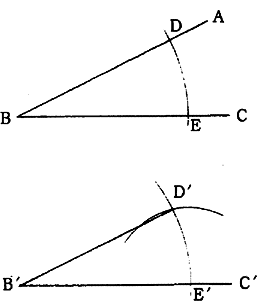
図1.12

前ページ　　　目次へ　　　次ページ